Uncinus is Latin for hooked and when applied to cirrus—itself Latin for a lock of hair—it nicely characterizes the cloud, below: formally, it is cirrus uncinus. A familiar name for these clouds is fallstreaks, for they are streaks of ice crystals falling from a cloud, one which was originally made of water drops.
The reason ice crystals fall from a parent cloud of water drops was discussed last October in a posting called fallstreaks. In the picture shown at that time, the crystals fell, more or less, straight down because the wind through which the crystals fell did not change much with height. Under circumstances when they don’t fall straight down, they often take a parabolic path, a shape that looks like a hook, thus, the name, uncinus. Why does cirrus so often assume a parabolic shape?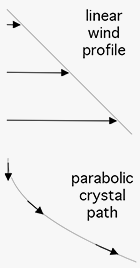
Curiously, the reason for the parabolic shape of uncinus is quite easy to account for using simple calculus, but is quite difficult to explain using simple English. This is just one of many situations where natural language falls short. Natural language often presents a view through a glass, darkly, under conditions that mathematics shows things face to face. Despite language limitations, here is an inevitably flawed attempt.
The ice crystals are all falling at roughly the same terminal velocity, but they fall though a wind that changes with height at a constant rate. Such a wind variation is common. One might expect that the streaks would take the same shape as this linear wind profile and so appear as a sloping straight line. This does not happen.
The problem is that each crystal falls through a succession of different winds and so its path is the cumulative effect of an acceleration from each level above it. The result is a streak with a parabolic shape. Of course, to the mathematically inclined, this is trivial: the integral of a linear function is a quadratic. (Another example of this behaviour is the parabolic path of a ballistic projectile, where the constant acceleration is not applied by a wind changing uniformly with height, but by gravity).
Often, the wind in the atmosphere changes at a constant rate with height. When ice crystals fall through such an atmosphere, the streaks are parabolic in shape. They look like a hooked lock of hair: cirrus uncinus.

Alistair, I like your explanation. Just a few comments (implied in the above):
1) The fall streaks will appear as a sloping straight line (i.e., have curvature zero) if the horizontal wind is constant with height.
2) The streaks will be strictly vertically aligned only if the upper wind is everywhere zero (which is quite rare).
3) The curvature of the streaks is maximum if you happen to look perpendicular to the upper wind.
Thanks again, fine topic.
Michael, you have to be the only one of my blog’s subscribers who has ever thought about this issue previously. Your point 3 is certainly correct. However, I will quibble with aspects of 1 and 2. An issue I glossed over in my writeup was the difference between the trajectory of a crystal and the shape of the streaks (the instantaneous position of the collection of crystals). What you said in 1 and 2 correctly applies to the trajectories, but not to the shape that is seen. A calculation of a trajectory is easy to make, but for it to give the same answer as the streak shape, the coordinate system must be chosen to move with the fallstreak, say by attaching the origin to its top. Once that is done, every wind that is constant with height has a zero velocity. A trajectory may trace out a diagonal line, but the shape of the streak is a vertical line because although all crystals move through space, they remain stacked one above the other. So, all winds that are constant with height correspond to case 2, which now does not turn out to be such a rare thing to see. And case 1 does not exist (well, it does for the trajectory, but not the shape that is seen).
I have always held dear to my mathematical heart that coordinate systems are by definition arbitrary and the liberty to strategically place the origin is an important insight for unmessy conception that must be constantly learned. Very nice distinction between the path of an ice particle and the visual effect of the moving group of particles. I would easily have missed this idea but I don’t still get why it wouldn’t be rare. If layers of wind are usually moving at different speeds (which I can readily imagine), wouldn’t that make the vertical, unhooked visual effect, rare? Your picture does indeed seem to show slightly curling incipient parabolic shapes suggesting slightly varying horizontal wind speeds blowing the ice particles.
Both comments above enjoyably erudite to any neophyte like me.
Doug, coordinate systems are indeed arbitrary, but as is widely known and was demonstrated here, some choices make for easy calculation, some don’t. In this case, only a coordinate system fixed to the fallstreak will result in all trajectories being the same and corresponding to the visual streaks. One can get the same result with any coordinate system but less intuitively and with greater effort. But, my primary point was that the calculation of a individual particle trajectory did not (without care) result in the calculation of the shape of a collection of particles
About the wind: winds that increase with height (below the jet stream) are the norm. Curiously, this is a result of the north-south temperature gradient (which in turn results from the shape of the Earth), a fact which produces pressure surfaces that slope downwards towards the poles, the slope of which increases with height. This results in winds that increase with height—just what is needed to produce the hooked fallstreaks. So, while one’s view of cirrus uncinus from the ground might be blocked by lower clouds, the hook shape is really common aloft.
As to winds that are (roughly) constant with height and so produce fallstreaks that hang vertically: these happen in a number of places meteorologically and geographically.
Alistair, you beat me. I still tried, assuming a nonlinear vertical wind profile, to get a linear fall streak that is yet inclined in the vertical; but I failed, and I can prove why. So we remain with your two cases:
1) Zero vertical wind shear: Fall streaks have curvature zero AND are strictly vertical.
2) Nonzero shear: Fall streaks are hooked (parabolic in case of linear shear).
Nothing seems to be in between. Thank you, good discussion.
Michael, nothing in between is certainly a non-intuitive result that nicely illustrates the point that mathematics can explore ideas that natural language cannot. And thank you; this discussion has instructed my own observing.
I burst out laughing at your correspondences, men. Priceless. Such pretty clouds.
Pamella, pretty clouds, indeed; a favourite of mine. Yet, the comments, while esoteric, were made by those with sufficient background in both math and physics to have a meaningful discussion on the form and behaviour of the cloud. Actually, there is even more that can be read from watching cirrus uncinus: one can even use it to determine the thermal advection aloft.