Making waves

It may seem odd that I consider the picture below to be special. As a shot of a muskrat swimming, it is distinctly ho-hum. But, as a shot characterizing water waves, it is long-sought superb. This demands an explanation. 

Almost any disturbance of a water surface, such as that caused by wind, swimming animal, or boat, will cause waves to travel out from the disturbance at some speed that is dependant upon the wavelength. For most of the waves we see — ones that buffet our boats — gravity is the restoring force and the longer the wave, the faster it travels. For the ripples (wavelength less than 1.7 cm), surface tension is the restoring force and the shorter the wave, the faster it travels. 

This dichotomy of wave behaviour has some strange consequences: 

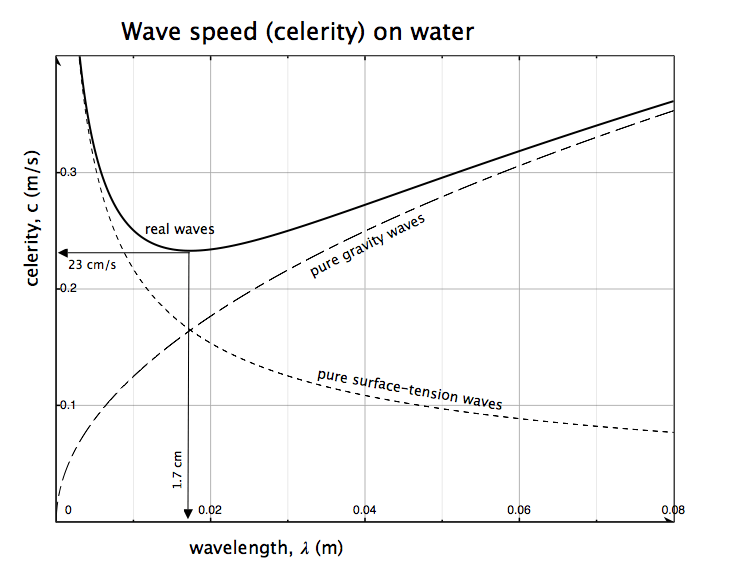
Real water waves (heavy line) are a combination of gravity waves and surface-tension waves. They must travel at greater than 23 cm/s.

• As the wave speed decreases owing to one mechanism, the other mechanism takes over and increases wave speed. Consequently, wave speed never drops below some value: 23 cm/s. So, something moving across a water surface at less than this baby crawl cannot produce waves that keep pace with it and so do not build and spread. The result is that such a slowly moving object leaves no spreading waves on the water surface. This behaviour was explored in a posting about katabatic winds, 23 cm/s.

• A disturbance moving faster than 23 cm/s will produce two types of waves: gravity waves and ripples. They are easily distinguished by having markedly different wavelengths, one much greater than 1.7 cm, the other much less. Mind you, if the speed of the disturbance is quite large (brisk wind, fast boat), the wavelength of the ripples may be so minute as to pass undetected.  

I have wanted to get a picture showing both types of waves simultaneously. A rapidly moving object, such as a dragon boat, would produce inconspicuous ripples and so won’t do. What is needed is something that moves only a bit faster than the no-wave cutoff: a muskrat. This misleadingly named aquatic vole is an inveterate surface swimmer as it searches for delectables to eat. It typically swims at slightly under its hull speed of about 70 cm/s (see, muskrat hull speed) and so is accompanied by easily distinguishable gravity waves and ripples.

Even though both wave forms are always present, it has proven difficult to obtain a picture that shows them equally. It is strictly a problem of good lighting and reflections to provide the necessary contrast needed to highlight both at once. Such a picture was achieved last Tuesday and is shown here.

A muskrat is swimming at nearly its hull speed of about 70 cm/s. The black bars on the right, and (not as striking) on the left are the crests of the gravity waves in its wake. Superimposed on these waves are the ripples. They are seen as the fine filigree ahead of the muskrat’s bow wave and nearly at right angles to the wake. A close examination of these ripples reveals their characteristic behaviour: the shortest wavelengths have travelled farthest as a result of having travelled fastest.